Data Structures & Algorithms in Java – Dynamic Programming – Longest Common Subsequence

Problem:

Given two strings , find the longest common subsequence between them.

For example ,

Consider the input:

“abcde” and “ace”

The longest common subsequence between them is “ace”.

A subsequence is just a sequence of characters from the original string with any characters removed and the order of remaining elements unchanged.

Try out the solution here:

https://leetcode.com/problems/longest-common-subsequence/

Solution:

Hint:

• Use Dynamic Programming – Iterate through each characters in both the strings and at each position compute the longest common subsequence by using the longest common subsequence for the previous characters.

Example:

Let’s consider the input:

“abcde” and “ace”

Lets draw a matrix using the above two strings. one string representing the row and another representing the column:

The first column and the first row are initialized to 0 .

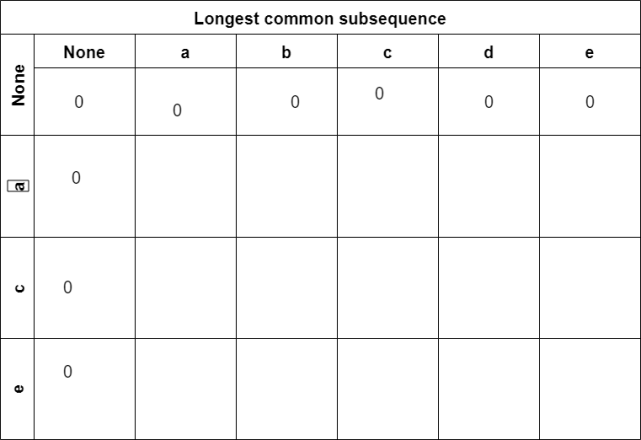
let the above matrix be represented as output[i][j] where i and j represent the row and column indices.

For each box in the above matrix , check if the characters match , if they match add 1 to the previous longest common subsequence present in 1 row and 1 column before.

That is ,

output[i][j] = output[i-1][j-1] +1

where output[i-1][j-1] is the length of the longest common subsequence without including the current characters from both the strings. Since the current character matches as well you increase the count and store it in this index.

If the characters don’t match , then find the longest common subsequence length without including these characters and find the maximum among them.

That is ,

output[i][j] = maximum of (output[i-1][j] , output[i][j-1])

Continue this for all the character combinations.

Here is the output of the matrix:

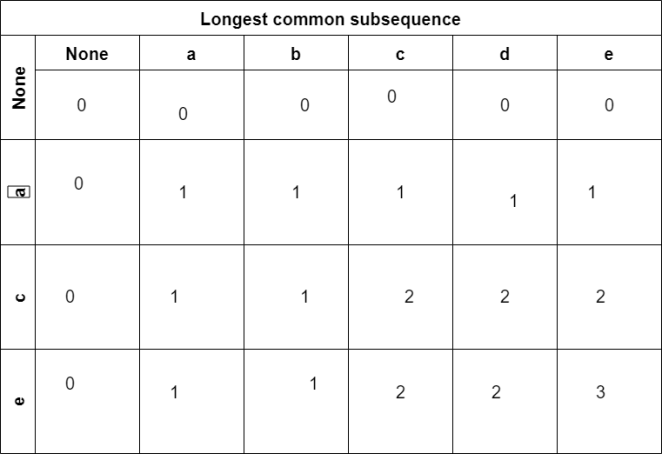
The final value in the matrix (3) represents the length of the longest common subsequence.

Algorithm:

STEP1: Initialize an output matrix

STEP2: For each character in each string inputs ,

STEP2a: If the characters match , add 1 to the longest common subsequence of the previous combination

STEP 2b: If the characters don’t match , find the maximum of the longest common subsequences without including each character.

STEP3: Return the value of the last combination

Code:

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        
        
        int[][] dp = new int[text1.length()+1][text2.length()+1];
        
        
        for(int i=0;i<text1.length();i++){
            
            
            for(int j=0;j<text2.length();j++){
                
                
                if(text1.charAt(i) == text2.charAt(j)){
                    
                    
                    dp[i+1][j+1] = dp[i][j]+1;
                }else{
                    
                    
                    dp[i+1][j+1] = Math.max(dp[i][j+1],dp[i+1][j]);
                }
            }
        }
        
        return dp[text1.length()][text2.length()];
    }
}

There is a minor change in the above code

when the characters match , the following code is executed:

dp[i+1][j+1] = dp[i][j]+1

This is because we start storing the output from index 1 instead of 0.

This is because if we use the below code:

dp[i][j] = dp[i-1][j-1]+1

The code will break when i = 0 and j = 0 , we need to handle them separately in that case. That can be avoided by starting with index 1 for both i and j. If you had noticed the initial array size is also one length and one breadth greater than the combination of the input strings lengths.

Time complexity of the above algorithm is O(m*n) where m and n are lengths of the two strings respectively.

Space complexity is also O(m*n) since we capture the combination of all possible strings in the output array.

That’s it!